判断一个单词是否是回文
思路:将字符串转换为数组,利用数组方法reverse()比较翻转后的字符串是否与源字符串一致。
实现:
function checkPalindrome(str) {
return str == str.split('').reverse().join('');
}
去掉一组整型数组重复的值
function uniqueArr(arr) {
var result = [];
for(var i = 0; i < arr.length; i++) {
if(arr.indexOf(arr[i]) === i) {
result.push(arr[i]);
}
}
return result;
}
uniqueArr([1,13,24,11,11,14,1,2]);//返回 [1, 13, 24, 11, 14, 2]
统计一个字符串出现最多的字母
function maxDuplicateLetter(str) {
//如果字符串仅有一个字符,即为该字符
if(str.length === 1) {
return str;
}
var letterObj = {};
for(var i = 0; i < str.length; i++) {
if(!letterObj[str[i]]) {//存放字母的对象中还未记录过该字母出现的次数
letterObj[str[i]] = 1;
}
letterObj[str[i]] += 1;
}
//接下来寻找存放字母的对象中最大的value所对应的key
var maxValue = 1;
var maxKey = '';
for(var key in letterObj) {
if(letterObj[key] > maxValue) {
maxValue = letterObj[key];
maxKey = key;
}
}
return maxKey;
}
maxDuplicateLetter("abcdddbb");//返回 "a"
排序算法
(1)冒泡排序
依次比较相邻两个数的大小,进行位置上的交换,若按由小到大排序,第一轮可以将最大的排在最右边。
平均时间复杂度:O(n^2) 最好情况:O(n) 最坏情况:O(n^2)
空间复杂度:O(1)
排序方式:In-place
稳定性:稳定
function bubbleSort(arr) {
for(var i = 0; i < arr.length; i++) {
for(var j = 0; j < arr.length - i -1; j ++) {
// 由小到大排序
if(arr[j] > arr[j + 1]){
var swap = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = swap;
}
}
}
return arr;
}
bubbleSort([3, 2, 4, 1, 7]);//返回 [1, 2, 3, 4, 7]
(2)快速排序
参考某个元素值,将小于它的值,放到左数组中,大于它的值的元素就放到右数组中,然后递归进行上一次左右数组的操作,返回合并的数组就是已经排好顺序的数组。
平均时间复杂度: O(n log n) 最好情况:O(n log n) 最坏情况:O(n^2)
空间复杂度:O(1)
排序方式:In-place
稳定性:不稳定
function quickSort(arr) {
if(arr.length <= 1) {
return arr;
}
var referValue = arr[0];
var leftArr = [];
var rightArr = [];
// 由小到大排序
for(var i = 1; i < arr.length; i++) {
if(arr[i] < referValue) {
leftArr.push(arr[i]);
} else {
rightArr.push(arr[i]);
}
}
return quickSort(leftArr).concat([referValue], quickSort(rightArr));
}
quickSort([3, 2, 4, 1, 7]);//返回 [1, 2, 3, 4, 7]
另外还有 选择排序、插入排序、希尔排序、归并排序、堆排序、计数排序、桶排序等,见博客js十大排序算法。
不借助临时变量,进行两个整数的交换
利用 + – 去进行运算,类似 a = a + ( b – a) 实际上等同于最后 的 a = b;
function swap([a, b]) {
var b = b - a;
var a = a + b;
var b = a - b;
return [a, b];
}
swap([2, 5]);//返回 [5, 2]
使用canvas 绘制一个有限度的斐波那契数列的曲线
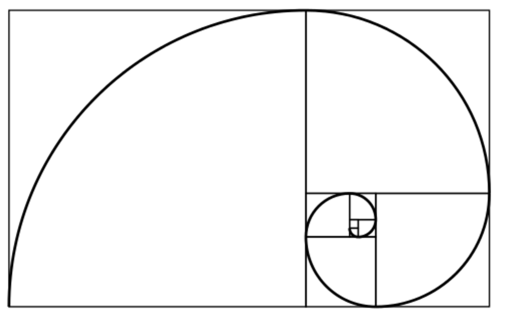
数列长度限定在9时的图像。
斐波那契数列,又称黄金分割数列,指的是这样一个数列:0、1、1、2、3、5、8、13、21、34、……fibo[i] = fibo[i-1]+fibo[i-2];
即生成斐波那契数列,然后再将该数列值作为半径,利用canvas arc方法绘制曲线。
function generateFibo(n) {
var fiboArr = [];
var i = 0;
while(i < n) {
if (i <= 1) {
fiboArr.push(i);
} else {
fiboArr[i] = fiboArr[i - 1] + fiboArr[i - 2];
}
i++;
}
return fiboArr;
}
generateFibo(6);//返回 [0, 1, 1, 2, 3, 5]
找出正数组的最大差值
相当于找到一个数组中的最大值与最小值,最大差值即为两者之差。
function maxDifference(arr) {
var minValue = arr[0];
var maxDiffer = 0;
for(var i = 0; i < arr.length; i++) {
minValue = Math.min(minValue, arr[i]);
currentDiffer = arr[i] - minValue;
maxDiffer = Math.max(maxDiffer, currentDiffer);
}
return maxDiffer;
}
maxDifference([10,5,11,7,8,9]);//返回 6
随机生成指定长度的字符串
function randomString(n) {
var rangeStr = 'abcdefghijklmnopqrstuvwxyz0123456789';
var l = rangeStr.length;
var randomStr = '';
for(var i = 0; i < n; i++) {
randomStr += rangeStr.charAt(Math.floor(Math.random() * l));
}
return randomStr;
}
randomString(10);//返回 "itfjah8rte"
实现类似getElementsByClassName 的功能
查找某个DOM节点下面的包含某个class的所有DOM节点?不允许使用原生提供的 getElementsByClassName、 querySelectorAll 等原生提供DOM查找的函数。
function queryClassName(node, name) {
var starts = '(^|[ \n\r\t\f])',
ends = '([ \n\r\t\f]|$)';
var resultArr = [],
reg = new RegExp(starts + name + ends),
elements = node.getElementsByTagName("*");
length = elements.length,
i = 0;
while(i < length) {
var element = elements[i];
if(reg.test(element.className)) {
resultArr.push(element);
}
i++;
}
return resultArr;
}
// 方法2
function queryClassName2(node, name) {
var elements = node.getElementsByTagName("*"),
length = elements.length,
resultArr = [];
for(var i = 0; i < length; i ++) {
if(elements[i].className) {
var classNames = elements[i].className.split(" ");/*这里其实还要考虑类名间隔大于一个空格的情况*/
if(classNames.indexOf(name) !== -1) {
resultArr.push(elements[i]);
}
}
}
return resultArr;
}
//HTML结构
<ul id="ull">
<li>0</li>
<li class='box box2'>1</li>
<li>2</li>
<li class='box1'>3</li>
<li class='box1'>4</li>
<li class='box box1'>5</li>
</ul>
//测试结果
window.onload = function() {
node = document.getElementById("ull");
queryClassName(node, "box");//返回 (2) [li.box.box2, li.box.box1]
queryClassName2(node, "box");// 返回 (2) [li.box.box2, li.box.box1]
};
JS 实现二叉查找树(Binary Search Tree)
在实际使用时会根据链表和有序数组等数据结构的不同优势进行选择。有序数组的优势在于二分查找,链表的优势在于数据项的插入和数据项的删除。但是在有序数组中插入数据就会很慢,同样在链表中查找数据项效率就很低。综合以上情况,二叉树可以利用链表和有序数组的优势,同时可以合并有序数组和链表的优势,二叉树也是一种常用的数据结构。
二叉查找树,也称二叉搜索树、有序二叉树(英语:ordered binary tree)是指一棵空树或者具有下列性质的二叉树:
任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
任意节点的左、右子树也分别为二叉查找树;
没有键值相等的节点。二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低。为O(log n)。二叉查找树是基础性数据结构,用于构建更为抽象的数据结构,如集合、multiset、关联数组等。
二叉树相关概念:
凡是每个节点都最多有两个叉的树,都叫二叉树。
查找树和排序树是一个东西。特点是中序遍历一遍的结果是单调的。这种树建出来可以用来做二分搜索。
平衡树一般是排序树的一种,并且加点条件,就是任意一个节点的两个叉的深度差不多(比如差值的绝对值小于某个常数,或者一个不能比另一个深出去一倍之类的)。
这样的树可以保证二分搜索任意元素都是O(log n)的,一般还附带带有插入或者删除某个元素也是O(log n)的的性质。
二叉树由节点(node)和边组成。节点分为根节点、父节点、子节点。如下图所示:
红色是根节点(root)。蓝色是子节点也是父节点,绿色的是子节点。其余的线是边。节点和链表中的节点一样都可以存放数据信息。树中的边可以用自引用表示,这种引用就是C/C++里面的指针。通常来说树是顶部小,底部大,且树呈分层结构。root节点时第0层,以此类推。二叉树最多有两个节点。
二叉树搜索: 二叉树一个节点左子节点的关键字小于这个节点,右子节点关键字大于或等于这个父节点。
创建一个树节点。
BST创建过程:
(1)创建一个树节点包括左节点引用和右节点引用。
(2)创建一个树结构。 创建一个树结构首先是向一个树种插入数据节点。当一棵树为null时,数据项是从树的root节点处开始插入,之后的插入顺序是根据搜索节点顺序规则进行插入。具体规则是:如果数据项比父节点的数据项要小,则插在父节点的左节点(leftNode),如果比父节点的数据项要大,则将新的node插入在父节点的右节点处(rightNode)。
插入数据节点过程如下所示:
插入节点的过程中其实也就是对tree遍历的过程,最终根据条件遍历到左右节点为null时进行添加新的节点。
查找关键字
查找关键字是数据结构一项重要操作项,在有序数组中通过二分排序效率非常高。在二叉树中的查找效率也比较高。因为二叉树的添加node的过程就是根据数据项的大小进行有序添加的,并不是毫无秩序的插入数据项。在有序的基础上进行查找关键字效率就会快很多。
树的最值查找在树中查找是比较容易的,因为从root开始查找,最小值只会出现所有父节点的左节点处,同样最大值只会出现在所有父节点的沿着右节点搜索的最底层右节点处。
参考自博客。
删除节点
给出如下二叉查找树

删除节点3之后,可以返回

或者

思路:
若要删除一个BST的一个结点,需要考虑如下三种情况:
需要删除的节点下并没有其他子节点
需要删除的节点下有一个子节点(左或右)
需要删除的节点下有两个子节点(既左右节点都存在)
对这三种情况分别采取的措施是:
直接删除此结点
删除此结点,将此结点父节点连接到此结点左(右)子树
找出此结点右子树中的最小结点,用以代替要删除的结点,然后删除此最小结点
设定每个节点的数据结构:
class Node {
constructor(data, left, right) {
this.data = data;
this.left = left;
this.right = right;
}
}
树由节点构成,由根节点逐渐延生到各个子节点,因此它基本的结构就是具备一个根节点,具备添加,查找和删除节点的方法。
// 构建BST,具备一个根节点、以及添加、查找、删除节点的方法
class BinarySearchTree {
constructor() {
this.root = null;
}
// 插入节点的方法
insert(data) {
let n = new Node(data, null, null);
if (!this.root) { //如果此二叉树为空,则数据项从树的root节点处开始插入
return this.root = n;
}
let currentNode = this.root;
let parent = null;
while (true) {
parent = currentNode; //保存当current变为null之前的那一个父节点
if (data < currentNode.data) { //插在父节点的左节点
currentNode = currentNode.left;
if (currentNode === null) { //不断向左node寻找是否为null
parent.left = n;
break;
}
} else { //插在父节点的右节点
currentNode = currentNode.right;
if (currentNode === null) {
parent.right = n;
break;
}
}
}
}
// 删除数据项
remove(data) {
this.root = this.removeNode(this.root, data);
}
// 删除节点
// 删除树中与给定值相同的节点,如果树中没有相同值的节点,则不做处理,应该保证处理之后的树仍是二叉查找树。
removeNode(node, data) {
if (node === null) { // 如果根节点为空
return null;
}
if (data === node.data) {
// 没有子节点,即node为叶子节点
if (node.left === null && node.right === null) {
return null;
}
// 要删除的节点下只有右节点
if (node.left === null) {
return node.right;
}
// 要删除的节点下只有左节点
if (node.right === null) {
return node.left;
}
// 要删除的节点下有两个子节点的情况
// getSmallest用于找到该节点右子树中的最小节点,用以替代要删除的节点,然后删除此最小节点
let getSmallest = function (node) {
if (node.left === null && node.right === null) {
return node;
}
if (node.left !== null) {
return node.left;
}
if (node.right !== null) {
return getSmallest(node.right);
}
}
let temNode = getSmallest(node.right);
node.data = temNode.data;
node.right = this.removeNode(temNode.right, temNode.data);
return node;
} else if (data < node.data) {
node.left = this.removeNode(node.left, data);
return node;
} else {
node.right = this.removeNode(node.right, data);
return node;
}
}
// 查找方法
find(data) {
let currentNode = this.root;
while (currentNode !== null) {
if (data === currentNode.data) {
return true;
}
if (data < currentNode.data) {
if (currentNode.left !== null) {
currentNode = currentNode.left;
} else {
return false;
}
} else {// data > currentNode.data
if (currentNode.right !== null) {
currentNode = currentNode.right;
} else {
return false;
}
}
}
}
}
有关数组的一些操作见博客后半部分前端面试中的常见的算法问题。
下面是一篇总结常见数据结构的javascript实现的文章:
常见数据结构的javascript实现。




